C++ Компьютерная графика

Построить дерево Аммерала

Задание
Построить дерево Аммерала.

В данной работе отражен вывод дерева Аммерала в среде программирования Borland С++ Builder 6 Enterprise. А так же разработка исходного кода вывода функции.

Пояснение. Идея алгоритма построения дерева принадлежит Аммералу. Сначала выводится прямоугольник, соответствующий стволу дерева. Затем на верхней стороне прямоугольника строится прямоугольный треугольник, для которого эта сторона служит гипотенузой. Затем на каждом из катетов полученного прямоугольного треугольника будут построены прямоугольники, и этот процесс будет рекурсивно применен к каждому из этих двух прямоугольников.

//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include <math.h>
#include "rgz2zd2.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
        : TForm(Owner)
{
}
//---------------------------------------------------------------------------
float xmin=-400, xmax=800; // масштаб по x
float ymin=200, ymax=1300; //мастштаб по у
const double PI=3.14159;
int maxX, maxY, zz=0;
float xdens, ydens;
int ex(float x){
	return (int) ((x-xmin)/xdens);
}
int ey(float y){
	return (int) ((ymax-y)/ydens);
}
//вывод отрезка
void line(int x0, int y0,int x1, int y1){
        Form1->Image1->Canvas->MoveTo(x0,y0);
        Form1->Image1->Canvas->LineTo(x1,y1);
}

// рекурсивная функция построения дерева
void piphagor(float x0,float y0,float x1, float y1){
	float x0s, y0s, x1s, y1s, x2s, y2s;
	float lambda= 1.+(2.-1.)*(0.+rand()%10000)/10000;
	float phi= PI/2 + (PI-PI/2)*(0.+rand()%10000)/10000;
	if((x1-x0)*(x1-x0)+(y1-y0)*(y1-y0)<1){
			line(ex(x0),ey(maxY-y0),ex(x1),ey(maxY-y1));
			return;
	}
	x0s= x0-lambda*(y1-y0); y0s= y0+lambda*(x1-x0);
	x1s= x1-lambda*(y1-y0); y1s= y1+lambda*(x1-x0);
     	line(ex(x0), ey(maxY-y0), ex(x0s), ey(maxY-y0s));
	line(ex(x1), ey(maxY-y1), ex(x1s), ey(maxY-y1s));
	x2s= (x0s+x1s)/2+ (x1s-x0s)/2*cos(phi)-(y1s-y0s)/2*sin(phi);
	y2s= (y0s+y1s)/2+ (x1s-x0s)/2*sin(phi)+(y1s-y0s)/2*cos(phi);
	piphagor(x0s,y0s,x2s,y2s);
	piphagor(x2s,y2s,x1s,y1s);
}

void __fastcall TForm1::trolo(TObject *Sender){
Form1->Image1->Picture->Bitmap->FreeImage();
Form1->Image1->Picture->Bitmap = NULL;
maxX=Form1->Image1->Width;
maxY=Form1->Image1->Height;
xdens=(xmax-xmin)/maxX;
ydens=(ymax-ymin)/maxY;
piphagor(maxX/2+40, 0, maxX/2-40, 0);
}

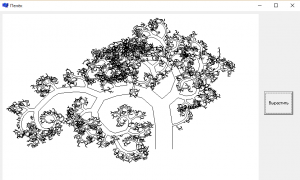
Вывод построенного дерева показан на рисунке 1.